Cacti: A/B Testing
For this project, I took two versions of the same website and sent them to my peers to use. I then examined the logs from their useage in order to measure the effect of the differences between the sites.
Two Site Designs:
Version A

Version B
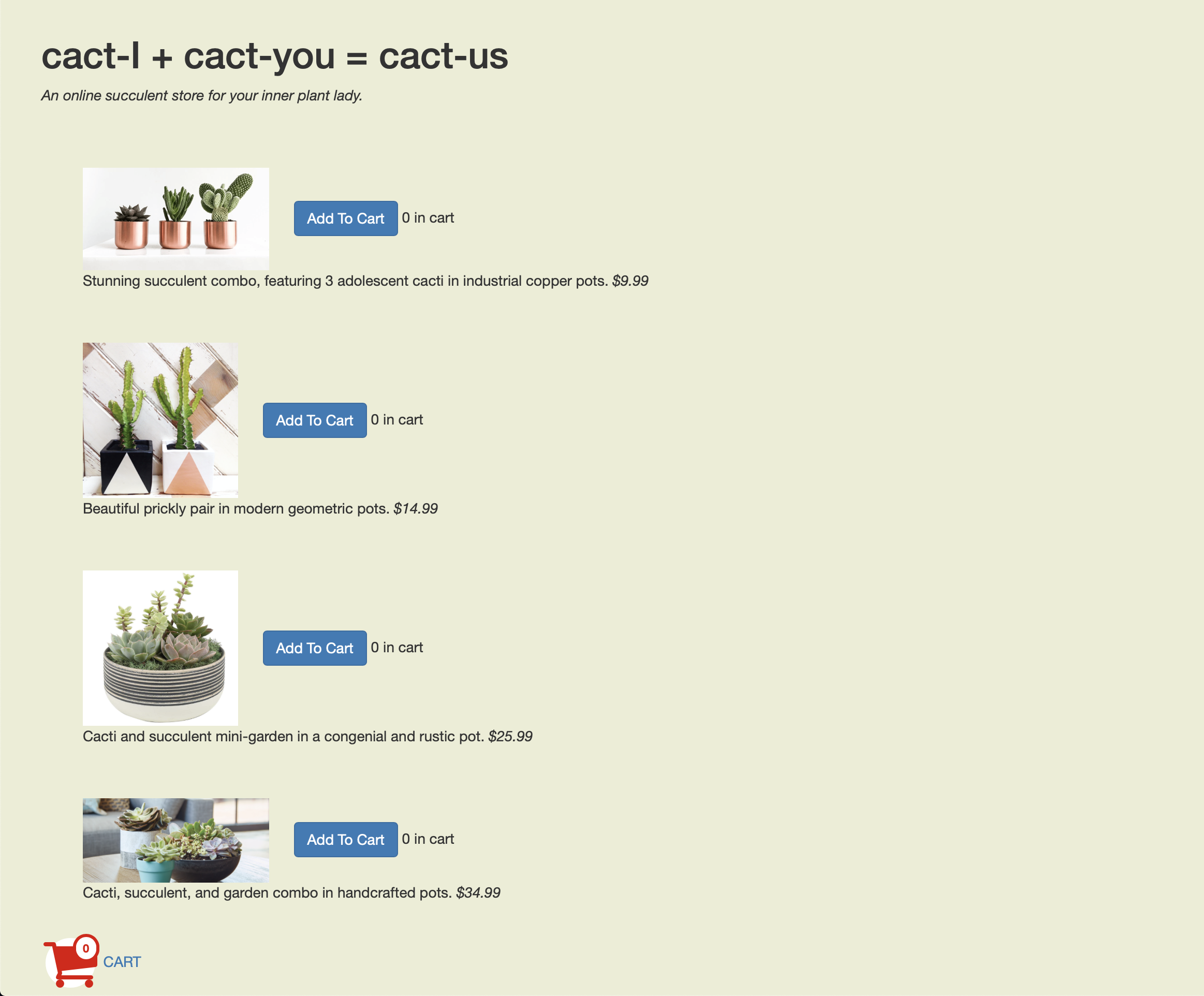
Differences
As you can see, version A of the webiste has a horizontal layout of the cacti, whereas version B has a vertical layout. Because of this difference, I hypothesize that the vertical layout will cause people to take more time to add items to their cart, as they will need to scroll to view all the items on most devices, rather than being able to see all of them initially.
Hypotheses
For the time to completion, my alternative hypothesis is that people will take more time to complete their actions on site version B than on version A. My null hypothesis is that there is not a statistically-significant difference between the times it takes people to complete their actions on the two sites.
For the return rate, my alternative hypothesis is that there will be a significant difference in the return rates between versions A and B. My null hypothesis is that there is no significant difference between the return rates.
Data Collection
To collect the data, I waited for my classNamemates to use the site in order to generate the useage data, and then I downloaded the sitelog from Heroku. After I downloaded the data, I filtered it and organized in in Excel in order to calculate the necessary values.
Test Results
Time to Completion Test
For the time to completion, I ran a t-test and found a significant difference between site A and site B, with my test producing a t-score of -3.3349 and a p-value of 0.0006, far less than the alpha of 0.05. This means that there was a statistically significant difference between the two populations and we can therefore reject the null hypothesis. Below you can see an infographic of the two populations, where you'll notice that the mean value for population A is lower than population B, meaning that users took less time to complete their tasks on version A.

Return Rate Test
For the return rate, I ran a chi-squared test which produced a chi-squared value of 0.1193 and a p-value of 0.7300, which is far higher than our alpha of 0.05. Because of this we fail to reject the null hypothesis, which means we have not found a significant difference between the two populations.
Takeaways
- Organizing items in a fashion that requires people to scroll more is correlated with people spending more time on your site, which may promote more thoughtful browsing than organizing items horizontally
- The limitation of this testing is that it was done over a short period of time, so we were not able to see who might have returned to the site over the long term.
- The number of users that accessed my site was not particularly large, so this could have impacted the results I received